PÉRDIDA DE CARGA EN TUBERÍA

Vídeo con el desarrollo de la práctica

Objetivo

Determinar la pérdida de carga que se produce en un tramo de tuberí­a aplicando el teorema de Bernoulli.

Fundamento teórico

Los fluidos que circulan por conducciones cerradas como tuberías, experimentan pérdidas de carga o energía.
El teorema de Bernoulli generalizado entre dos puntos es:

\(H_{1}=H_{2}+ΔH\)

Donde,
H_i: energía en un punto (m.c.a.)
ΔH: pérdida de carga (m.c.a.)

Sabiendo que:

\(H=z+\frac{ρ}{γ}+\frac{v^{2}}{2g}\)

Donde,
H: energía (m.c.a.)
z: cota al nivel de referencia (m)
ρ/γ: altura de presión (m.c.a.)
v²/2g: altura cinemática (m.c.a.)

Se podrán estudiar dos tipos de pérdida de carga en distintos puntos de la tubería:

• Pérdida de carga continua: Ecuación de Darcy para pérdida de carga unitaria por fricción.
• Pérdidas de carga localizada: válvulas, codos y cambios de sección.

 

Materiales

• Banco hidráulico.
• Bomba de agua.
• Equipo de fricción de tuberías.

 

Datos

• Diámetro interior (tubería a estudio): 17 mm.
• Longitud del tramo a estudio: 1 m.
• Caudal: 2000 l/h.
• Peso especí­fico del agua (γ_agua): 1000 kp/m³ (ST).
• Peso especí­fico del mercurio (γ_Hg): 13600 kp/m³ (ST).

 

Desarrollo

Se pone en marcha el banco hidráulico. El agua circulará en sentido ascendente hasta el equipo de fricción de tuberías gracias a la bomba.
Para que el agua circule por la tubería a estudio, basta con abrir y cerrar las válvulas pertinentes.

Una vez el agua esté circulando por la tubería y haya salido el aire que pudiese contener en su interior, se mide la presión en los puntos de inicio y final del tramo a estudio con el manómetro.

Para obtener la energía en cada punto (H_i) y evaluar la pérdida de carga total (ΔH), se procede de la siguiente forma:

• Obtener la presión en los dos puntos:

-Se realiza la lectura del manómetro en el punto 1,  tal y como se muestra en el esquema; siendo “a” la distancia de la lámina de agua (h_agua) y “b” la del mercurio (h_Hg).

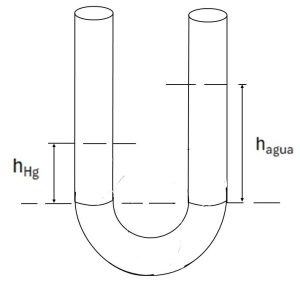
-Igualando presiones en la línea de referencia, P₁ se deduce de la siguiente expresión:

\(P_{i}=h_{Hg}·γ_{Hg}- h_{agua}·γ_{agua}+P_{ATM}\)

Donde,
Pi= presión en un punto de la tubería (kp/m²)(ST)
h_Hg= altura de la lámina de mercurio (m)
γ_Hg= peso específico del mercurio (kp/m³)(ST)
h_agua= altura de la lámina de agua (m)
γ_agua= peso específico del agua (kp/m³)(ST)
P_ATM= presión atmosférica (P_ATM= 0 kp/m²)

Se obtiene la presión en el punto 2 (P₂) de la misma forma.

Se observa que las presiones son diferentes por la pérdida de carga experimentada.

• Para obtener la velocidad en un punto basta con conocer el caudal (Q) y la sección de la tubería en dicho punto:

 

\(Q=v·S\)

Donde,
Q: caudal (m³/s)
v: velocidad (m/s)
S: sección (m²)

• Hallar la energía de cada punto (H_i) sustituyendo en la expresión de Bernoulli.
• Sustituir en la expresión generalizada de Bernoulli para hallar ΔH.

Se pueden probar distintas tuberías del banco, estudiándose así qué ocurre según las características que tenga la zona de estudio.

Formulario

Pérdida de carga total:

\(ΔH=ΔH_{c}+ΔH_{L}\)

Donde,
ΔH_c: pérdida de carga continua por fricción
ΔH_L: pérdida de carga localizada

• Pérdida de carga por fricción, ΔH_c:

\(ΔH_{c}=J·L\)

Donde,
J: pérdida de carga unitaria (m/m)
L: longitud del tramo (m)

Ecuación de Darcy :

\(J=\frac{f}{D}·\frac{v^{2}}{2g}\)

Donde,
f: coeficiente de fricción
D: diámetro de la tubería (m)
v: velocidad (m/s)

-Para el cálculo del coeficiente de rozamiento se utiliza el ábaco de Moody o la siguiente ecuación:

La ecuación de Colebrook-White:

\(\frac{1}{\sqrt{f}}=-2·log\left(\frac{2.51}{Re·\sqrt{f}}+\frac{\epsilon}{3.71·D}\right)\)

Donde,
∈=rugosidad absoluta (m)
Re= número de Reynolds

-A su vez, el número de Reynolds se calcula con la siguiente fórmula:

\(Re=\frac{D·v}{\nu}\)

Donde,
ν: viscosidad cinemática (m²/s)

• • La pérdida de carga localizada se obtiene a partir de la siguiente expresión:

 

\(ΔH_{L}=k·\frac{v^{2}}{2g}\)

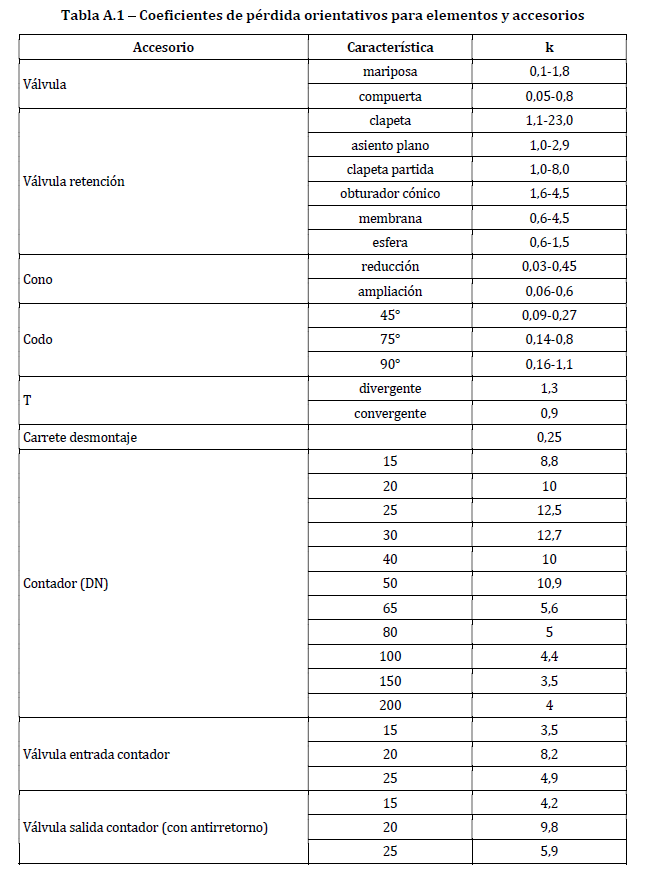
Donde el coeficiente de pérdidas k,  puede obtenerse de la siguiente tabla extraída de la UNE 149201:2017, según el tipo de accesorio:

Resultados

1. Tomando las presiones en dos puntos de la tuberí­a (mediante manómetro de mercurio), determinar la pérdida de carga que se produce entre estos dos puntos.

2. Comprobar cómo influyen los accesorios en la pérdida de carga en diferentes tuberías a estudio.

3. Comprobar cómo afecta un mayor o menor diámetro a la pérdida de carga continua (ecuación de Darcy).

4. Documentar teóricamente el ejercicio realizado.

 

Vídeo con el desarrollo de la práctica