Cuando se quiere estudiar el comportamiento del flujo en un conducto, muchos estudios y fórmulas hacen referencia a conductos circulares en el que el parámetro fundamental es el Diámetro.

Pero ¿Qué sucede si el conducto es rectangular, cuadrado, trapecial o de cualquier otra forma? En ese caso se recurre al denominado Diámetro Hidráulico Dh.

Cuando el flujo circula por un conducto, si hacemos una sección transversal, vemos que ocupa un área y que entra en contacto con las paredes a todo lo largo de la sección.

Debido a la rugosidad de las paredes, en la zona de contacto la velocidad es cero, y afecta enormemente a las pérdidas de energía que se produce durante la circulación del flujo. La longitud de contacto se denomina Perímetro Mojado.

La consecuencia, es que cuanto mayor contacto se tiene con las paredes mayor será la pérdida de energía que se producirá en relación con el Área mojada que ocupa el fluido al circular.

El factor que se utiliza se denomina Radio Hidráulico Rh y viene definido por la fórmula;

\(R_{h}=\frac{A_m}{P_m}\)

En el caso de una sección circular, definimos primeramente la geometría.

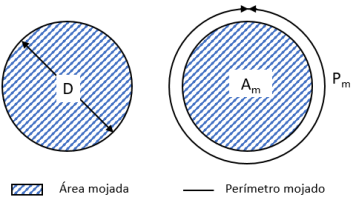
Aplicando la fórmula anterior, el Radio Hidráulico será;

\(R_{h}=\frac{A_{m}}{P_{m}}=\frac{\frac{\pi\cdot D^{2}}{4}}{\pi\cdot D}=\frac{D}{4}\)

De esta forma, tenemos que el Diámetro del conducto circular se relaciona con el concepto de Radio Hidráulico por la ecuación:

\(D=4\cdot R_{h}\)

Este diámetro es el que se denomina Diámetro Hidráulico \(D_{h}\).

De esta forma se puede relacionar el concepto de Radio Hidráulico de un conducto no circular con el que le corresponde a un conducto circular y así poder asemejar el comportamiento al de un conducto de sección circular.

Por ejemplo, en el caso de una sección rectangular, la definición geométrica será;

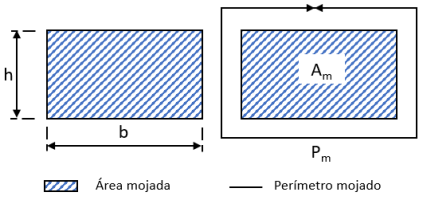
Aplicando el concepto de Radio Hidráulico, tenemos;

\(R_{h}=\frac{A_{m}}{P_{m}}=\frac{b\cdot h}{2\cdot b+2\cdot h}\)

Igualando el Radio Hidráulico del conducto circular y el del conducto rectangular, tenemos;

\(D=4\cdot R_{h}=4\cdot \frac{b\cdot h}{2\cdot b+2\cdot h}=\frac{4\cdot b\cdot h}{2\cdot\left(b+h\right)}\rightarrow D=\frac{2\cdot b\cdot h}{b+h}\)

En resumen. Si tomamos como referencia el concepto de Radio Hidráulico y lo igualamos al del conductor circular, podremos obtener el Diámetro Hidráulico de cualquier sección.

\(D=4\cdot R_{h}=4\cdot \frac{A_{m}}{P_{m}}\)

O de la forma conocida generalmente,

\(D_{h}=4\cdot \frac{A_{m}}{P_{m}}\)

Ahora que ya sabemos el fundamento, realizamos un ejemplo práctico.

Ejemplo 1

Sea el conducto cuadrado de 500 mm de lado, calcular el Diámetro Hidráulico.

El área de un cuadrado es \(l · l\), por tanto, el Área mojada es:

\(A_{m}=l\cdot l=0.5\cdot 0.5=0.25\ m^{2}\)

El perímetro del cuadrado es \(4\cdot l\), por tanto, el perímetro mojado es:

\(P_{m}=4\cdot l=4\cdot 0.5=2\ m\)

El Radio Hidráulico es;

\(R_{h}=\frac{A_{m}}{P_{m}}=\frac{0.25}{2}=0.125\ m\)

Como el Diámetro Hidráulico es 4 veces el Radio Hidráulico, tenemos;

\(D=4\cdot R_{h}=4\cdot 0.125 = 0.5\ m\)

Ejemplo 2

Sea un conducto anular de diámetro exterior 0.4 m, e interior de 0.3 m, calcular el Diámetro Hidráulico.

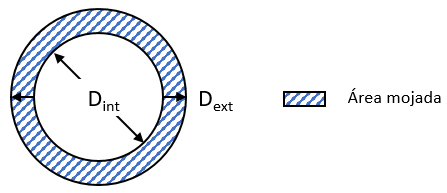
El Área mojada se calcula como diferencia del área del círculo mayor menos el área del círculo menor;

\(A_{m}=\frac{\pi\cdot D_{ext}^2}{4}-\frac{\pi\cdot D_{int}^2}{4}=\frac{\pi}{4}\cdot \left(D_{ext}^2-D_{int}^2\right)\)

El Perímetro corresponde con la zona de contacto del agua con las paredes. Por tanto, será la suma de ambos;

\(P_{m}=\pi\cdot D_{ext}+\pi\cdot D_{int}=\pi\cdot \left( D_{ext}+D_{int}\right)\)

Quedando el Radio Hidráulico;

\(R_{h}=\frac{S_{m}}{P_{m}}=\frac{\frac{\pi}{4}\cdot \left(D_{ext}^2-D_{int}^2\right)}{\pi\cdot \left( D_{ext}+D_{int}\right)}=\frac{{\pi}\cdot \left(D_{ext}^2-D_{int}^2\right)}{4\cdot \pi\cdot \left( D_{ext}+D_{int}\right)}=\)

\(=\frac{\left( D_{ext}+D_{int}\right)\cdot\left(D_{ext}-D_{int}\right)}{4\cdot \left( D_{ext}+D_{int}\right)}=\frac{1}{4}\cdot\left(D_{ext}-D_{int}\right)\)

Como el Diámetro Hidráulico es cuatro veces el Radio Hidráulico, tenemos;

\(D_{h}=4\cdot R_{h}=4\cdot \frac{1}{4}\cdot\left(D_{ext}-D_{int}\right)=D_{ext}-D_{int}\)

Sustituyendo los valores del enunciado queda;

\(D_{h}=D_{ext}-D_{int}=0.4-0.3=0.1\ m\)